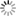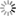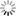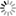Intrinsic parameters of each camera composing the stereo system are calibrated using a hand crafted known target (i.e., a chessboard). Since we expect such target being generally affected by some imperfections (i.e. printing misalignments, small bumps or glitches) we implemented the method described in Albarelli et al. (2010) that suggest a bundle adjustment step to optimize both camera parameters and target geometry. Each camera is therefore calibrated independently by acquiring ~50 snapshots of the target with different orientation and distance from the camera, spanning a space about 3 m depth and 5 m wide in front of it. All the parameters are estimated by imposing zero skewness, square pixels, and a five coefficients polynomial radial distortion model.
The estimation of the intrinsic parameters is not enough to perform the stereo reconstruction from a pair of images. In fact, the reciprocal position of the two cameras (the so-called extrinsic parameters) must be provided to recover the full geometry of the scene through triangulation. The extrinsic parameters define the displacement τ and the rotation R between the left and right camera frames according to the Euclidean transformation g = (R, τ). In previous WASS deployments, the rigid motion g was estimated by exposing an ad-hoc calibration target to both cameras, and by relating the known 3-D geometry of the target with its re-projection onto the image planes. However, even if this is the standard de-facto way to calibrate a stereo rig in laboratory conditions, this approach manifests several drawbacks when applied to stereo systems with large baseline.
At first, since for field applications we usually require a baseline τ between cameras larger than 2 m, the target size has to be wider than 1x1 m2, and placed at a distance greater than about 5 m from the cameras. Due to the target size, the manufacturing process may lead to some coarse imperfections and allowing the protrusion of such target meters away from the vessel hull can be time consuming or even dangerous. Moreover, the calibration procedure is time intensive and requires taking apart the device from its working position. As such, it is very difficult to modify the system geometry on-the-fly to accommodate different acquisition requirements. For instance, it may be reasonable to take the device closer to the sea when the waves are slight, so a small but highly resolved sea surface region can be acquired. On the other hand, large waves demand a broader area, requiring the device to be repositioned farther from the surface. Finally, the “calibrate once and for all” strategy is not reliable since vibrations of the support and environmental factors, as wind, can modify the relative angle between cameras and jeopardize the reconstruction accuracy.
To overcome these limitations, we developed a calibration procedure that relies on the photometric consistency of the sea surface itself, and thus can be carried out during the acquisition without the need of a calibration target. Specifically, it is well known that it is possible to estimate the relative pose of two cameras, up to scale, from a set of corresponding points between the two images (Figure).
Estimation of the stereo camera pose: example of corresponding features in the two stereo-camera images. In the left and right images corresponding pixels are connected with a yellow line. Stereo images are taken by a WASS mounted on the “Acqua Alta” oceanographic platform (northern Adriatic Sea, Italy).
Therefore, taking some points (in homogeneous coordinates) p_1…p_n extracted from a frame captured by the first camera (say left), and the corresponding set p_1^'…p_n^' by the second (say right), the epipolar constraint can be exploited to estimate the essential matrix M such that (Ma et al., 2004)
p_i M p_i^'= 0,∀i = 1…n
Moreover, the essential matrix can be decomposed through singular value decomposition to recover the rigid motion g up to a scale factor for τ (Hartley and Zisserman, 2004). While conceptually simple, determining such corresponding points can be a difficult task particularly when dealing with un-textured areas or repetitive patterns. Not surprisingly, sea surface is not rich of distinctive features so special care has to be taken to let this process be as reliable as possible. In the stereo pipeline, the extrinsic calibration process starts with the extraction of a set of Speeded Up Robust Features (SURF; Bay et al., 2008) from each image. The algorithm is set to use 3 octaves, 8 intervals per octave and a blob response threshold of 10-4. To obtain a more uniform spatial distribution of interest points in a frame, the image is divided in 16 blocks and points with lower hessian response are iteratively removed from each block to finally collect a set of 2600 features for each image. From these feature points, orientation, scale and a 64-components descriptor are computed.
Since most of these points are located on high textured areas (waves crest and white capped areas), the descriptor itself is not sufficient to establish a reliable set of matches between left and right camera features. Indeed, the local information around each point is not distinctive when dealing with a surface that shows uniform color, smooth shading, and clear but repetitive white areas. To guarantee a good set of point-to-point correspondences, we implemented the state-of-the-art method proposed in Albarelli et al. (2012). The key idea is that, for small motions, the transformation between stereo images that affects a group of close-by features can be approximated to be affine. Therefore, scale and orientation of each interest point may be used to define the similarity between two possible candidate matches as a function of their coherence with respect to the same affine transformation. To filter consistent sets of matches that are all mutually compatible, a non-cooperative evolutionary game is repeated many times to extract up to 30 groups with more than 5 matches each. After the inlier selection, most of the filtered correspondences are correct. We are able to obtain an average of 150 matches for each couple of left-right frames.
To make the process even more robust, we embedded the subsequent essential matrix estimation step inside a RANSAC (Random Sample Consensus) scheme to guarantee that the computed matrix is coherent with a large enough set of features. Specifically, we start by merging together all matches extracted from a sequence of n consecutive frames. From this set of matches, we iteratively extract 5 random elements and estimate all possible essential matrices (in general, with only five points there are many different solutions) by using the method presented in Nister (2004). These essential matrices hypothesis are used to count how many points have its relative match nearer than one pixel from the corresponding epipolar line. After 50000 iterations, the essential matrix coherent with the largest number of matches is kept, and used to recover rotation and translation.
Due to the low rank of the essential matrix, the motion is recovered up to scale, i.e. the magnitude of the translation vector τ is arbitrary. Since for wave measurements it’s crucial to provide reconstructions with the correct scale, we estimate such parameter by showing a known object to both the cameras. Despite being conceptually similar to the use of a calibration target, the estimation of the scale parameter alone is a very well-conditioned problem and thus it does not require a complex reference object. Indeed, we use an object of known shape that is captured for several consecutive frames. The ratio between the reconstructed 3-D object and its known dimensions gives the scale factor that has to be applied to the vector τ to fix the baseline. Even if this estimation can be done just with a single stereo shot, we averaged the scale computed for a set of multiple frames weighted by the area of the object projection on each image. This leads to a more robust estimation.
The estimation of the intrinsic parameters is not enough to perform the stereo reconstruction from a pair of images. In fact, the reciprocal position of the two cameras (the so-called extrinsic parameters) must be provided to recover the full geometry of the scene through triangulation. The extrinsic parameters define the displacement τ and the rotation R between the left and right camera frames according to the Euclidean transformation g = (R, τ). In previous WASS deployments, the rigid motion g was estimated by exposing an ad-hoc calibration target to both cameras, and by relating the known 3-D geometry of the target with its re-projection onto the image planes. However, even if this is the standard de-facto way to calibrate a stereo rig in laboratory conditions, this approach manifests several drawbacks when applied to stereo systems with large baseline.At first, since for field applications we usually require a baseline τ between cameras larger than 2 m, the target size has to be wider than 1x1 m2, and placed at a distance greater than about 5 m from the cameras. Due to the target size, the manufacturing process may lead to some coarse imperfections and allowing the protrusion of such target meters away from the vessel hull can be time consuming or even dangerous. Moreover, the calibration procedure is time intensive and requires taking apart the device from its working position. As such, it is very difficult to modify the system geometry on-the-fly to accommodate different acquisition requirements. For instance, it may be reasonable to take the device closer to the sea when the waves are slight, so a small but highly resolved sea surface region can be acquired. On the other hand, large waves demand a broader area, requiring the device to be repositioned farther from the surface. Finally, the “calibrate once and for all” strategy is not reliable since vibrations of the support and environmental factors, as wind, can modify the relative angle between cameras and jeopardize the reconstruction accuracy.To overcome these limitations, we developed a calibration procedure that relies on the photometric consistency of the sea surface itself, and thus can be carried out during the acquisition without the need of a calibration target. Specifically, it is well known that it is possible to estimate the relative pose of two cameras, up to scale, from a set of corresponding points between the two images (Figure).Estimation of the stereo camera pose: example of corresponding features in the two stereo-camera images. In the left and right images corresponding pixels are connected with a yellow line. Stereo images are taken by a WASS mounted on the “Acqua Alta” oceanographic platform (northern Adriatic Sea, Italy).Therefore, taking some points (in homogeneous coordinates) p_1…p_n extracted from a frame captured by the first camera (say left), and the corresponding set p_1^'…p_n^' by the second (say right), the epipolar constraint can be exploited to estimate the essential matrix M such that (Ma et al., 2004)p_i M p_i^'= 0,∀i = 1…nSince most of these points are located on high textured areas (waves crest and white capped areas), the descriptor itself is not sufficient to establish a reliable set of matches between left and right camera features. Indeed, the local information around each point is not distinctive when dealing with a surface that shows uniform color, smooth shading, and clear but repetitive white areas. To guarantee a good set of point-to-point correspondences, we implemented the state-of-the-art method proposed in Albarelli et al. (2012). The key idea is that, for small motions, the transformation between stereo images that affects a group of close-by features can be approximated to be affine. Therefore, scale and orientation of each interest point may be used to define the similarity between two possible candidate matches as a function of their coherence with respect to the same affine transformation. To filter consistent sets of matches that are all mutually compatible, a non-cooperative evolutionary game is repeated many times to extract up to 30 groups with more than 5 matches each. After the inlier selection, most of the filtered correspondences are correct. We are able to obtain an average of 150 matches for each couple of left-right frames.To make the process even more robust, we embedded the subsequent essential matrix estimation step inside a RANSAC (Random Sample Consensus) scheme to guarantee that the computed matrix is coherent with a large enough set of features. Specifically, we start by merging together all matches extracted from a sequence of n consecutive frames. From this set of matches, we iteratively extract 5 random elements and estimate all possible essential matrices (in general, with only five points there are many different solutions) by using the method presented in Nister (2004). These essential matrices hypothesis are used to count how many points have its relative match nearer than one pixel from the corresponding epipolar line. After 50000 iterations, the essential matrix coherent with the largest number of matches is kept, and used to recover rotation and translation.Due to the low rank of the essential matrix, the motion is recovered up to scale, i.e. the magnitude of the translation vector τ is arbitrary. Since for wave measurements it’s crucial to provide reconstructions with the correct scale, we estimate such parameter by showing a known object to both the cameras. Despite being conceptually similar to the use of a calibration target, the estimation of the scale parameter alone is a very well-conditioned problem and thus it does not require a complex reference object. Indeed, we use an object of known shape that is captured for several consecutive frames. The ratio between the reconstructed 3-D object and its known dimensions gives the scale factor that has to be applied to the vector τ to fix the baseline. Even if this estimation can be done just with a single stereo shot, we averaged the scale computed for a set of multiple frames weighted by the area of the object projection on each image. This leads to a more robust estimation.