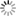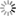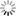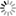3-D reconstruction
With the device calibrated, each image pair is stereo rectified and processed by a modified version of the dense stereo algorithm proposed by Hirschmüller (2008) available in the OpenCV library (Bradski & Kaehler, 2008; http://opencv.org), in order to match (with sub-pixel accuracy) all the pixels of the two stereo images (Figure). The semi-global nature of the approach has the great advantage that it can relate the photometric consistency of several matching pixels to improve the reliability of the disparity map, especially for areas with loosely distinctive features. As a consequence, we can keep a relatively small window size (13x13 pixels) while still obtaining a precise localization of the matches. This corrects the matching bias in points around white-capped areas (Leckler et al. 2015) without introducing brightness equalizations or articulated pyramidal search approaches.
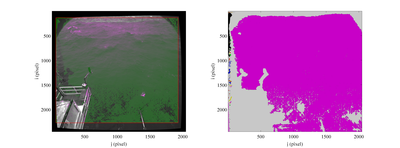
After the dense stereo process, a 3-D scattered point cloud is obtained for each frame pair. Even if the algorithm already filters the disparity map to reduce the noise of the produced output, its effectiveness is limited, as it cannot make assumptions on the reconstructed scene. Conversely, we expect the sea surface to be continuous and smooth everywhere. To greatly reduce the number of point outliers we use an additional filtering step taking advantage of the surface smoothness along the camera optical z-axis. We start by building a graph (Figure 2) with the vertices being the reconstructed points and edges connecting each vertex with its 4-neighbours considering the adjacency relation of points induced by the image topology. For each edge, a weight is computed as the absolute difference of the z-components of their respective points coordinates. Then, each edge whose weight is greater than the 98th percentile of the weight distribution is pruned by the graph. The idea is to disconnect all the vertices exhibiting abrupt changes along the z-axis with respect to the neighbors. Finally, we filter out all the 3-D points not belonging to the biggest connected component of the graph.Dense stereo reconstruction: example of disparity coverage (left panel) and graph component (right panel) in the right image plane. On the right panel, the biggest connected component of the graph is shown as purple region. Stereo images are taken by a WASS mounted on the “Acqua Alta” oceanographic platform (northern Adriatic Sea, Italy).